TAO - Getting Started

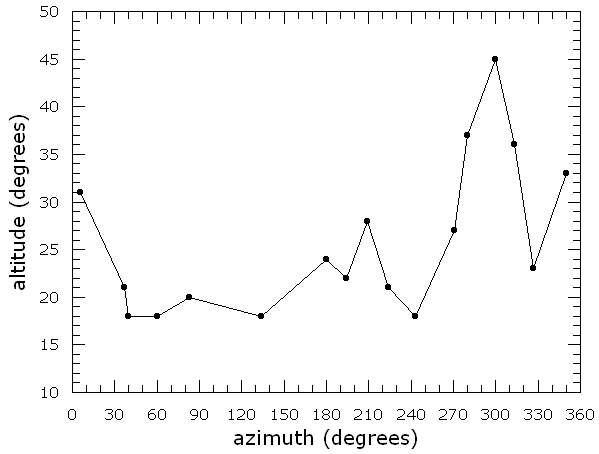
Step 5: Modeling the local horizon

This step is more conveniently done in daytime when one can see the horizon obstructions more clearly. The horizon measurements are made by pointing the telescope at various points along the local horizon, and recording the altitude (in degrees) and azimuth (in degrees, measured north through east, from 0 to 360 deg) of each point. The points should be more closely spaced at those portions of the horizon where the altitude changes more rapidly with azimuth (e.g., trees, house walls, etc.). A relatively complex sample horizon line is show below.

The azimuth and altitude data for the local horizon line should be entered in a text file (horizon model), with the following format:

! Example horizon model
!
! August 19, 2004
!
! Azimuths (first column) and altitudes (second column) are given in
! degrees. Azimuth is measured from North (0 deg) through East (90 deg),
! and varies from 0 to 360 deg. Data points must be listed in order
! of ascending azimuth.

  6.   31.
 37.   21.
 40.   18.
 60.   18.
 83.   20.
134.   18.
180.   24.
194.   22.
209.   28.
224.   21.
243.   18.
271.   27.
280.   37.
300.   45.
313.   36.
327.   23.
350.   33.

In a horizon model, comment lines start with "!" and are ignored; blank lines are also ignored.

Horizon models are usually saved to directory TAO\schedule. This sample horizon model (TAO\schedule\horizon.txt) may be used as a template for creating your own horizon models. If you use more than one telescope, each one may have its own local horizon line.

Notes:

When computing the horizon altitude for an arbitrary azimuth, the TAO scheduler performs a linear interpolation on the data points contained in the horizon model file. That is the reason why the data points must be more closely spaced in those parts of the horizon line where the altitude changes more rapidly with azimuth.

If you wish to prevent observations on one side of the meridian, you may set the horizon altitude to 90 deg for all azimuths corresponding to that side of the meridian. In this way, to prevent observations on the west side of the meridian (azimuths between 180 and 360 deg), the horizon model might look like this:

  0.01	19.5
  2.5	24.5
  ...   ...
179.99  35.2
180.0   90.0
360.0   90.0

(note the abrupt change in altitude near azimuths 0 and 180 deg).

If you have a non-automated dome, it is even possible to model the shutter's edges as seen from inside the stationary dome as a "horizon line", so that the TAO scheduler will only schedule observations of objects as they pass in front of the open shutter. Different horizon model files might be prepared to describe the shutter's edges when it points at different azimuths. This ingenious artifice has been suggested and used by C. Jacques (MPC Observatory Code 859).

TAO currently assumes that each constant azimuth line intercepts the local horizon line at exactly one point. This does not allow the accurate modeling of certain complex obstructions which are wider at the top than at the base or which have holes. An example of an obstruction of the first kind would be a tall palm tree; in this case, only the top of the tree's canopy could be accurately modeled, while the visible portions of the sky below the canopy would become effecively unobservable (since no observations are scheduled below the model horizon line). An example of an obstruction of the second kind would be a tree's canopy with a hole in it. Again the top of the canopy could be accurately modeled, but no observations would ever be scheduled to take place through the hole. Future versions of TAO may allow more general horizon lines.